L’area del cerchio è un concetto fondamentale in geometria che ha applicazioni pratiche in vari settori della scienza e dell’ingegneria. Comprendere come calcolare l’area del cerchio non solo è essenziale per gli studi matematici, ma anche per la risoluzione di problemi pratici in diverse discipline. In questo articolo, esploreremo la formula per calcolare l’area del cerchio, le sue proprietà principali, e le sue applicazioni reali In questo articolo, esploreremo in dettaglio il concetto di “area del cerchio”, analizzando la formula utilizzata per il calcolo, le sue applicazioni pratiche e alcuni esempi che illustrano l’importanza di questa misura nella vita quotidiana. Scopriremo anche come la comprensione di questa area possa facilitare una varietà di compiti e progetti, rendendo la matematica non solo più accessibile ma anche più rilevante.

2. Concetti Fondamentali
Cos’è un cerchio?
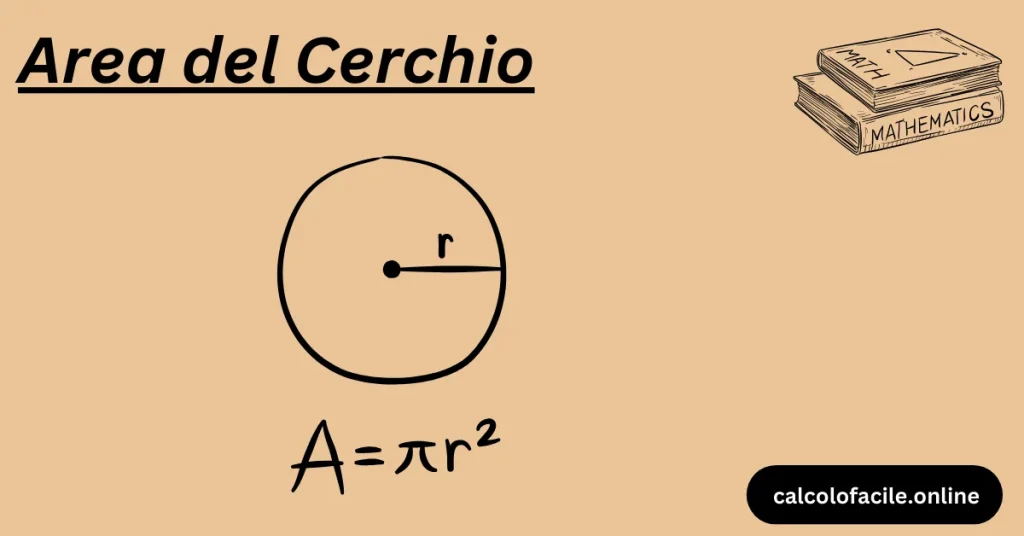
Un cerchio è una figura geometrica piana costituita da tutti i punti equidistanti da un punto centrale, chiamato centro. La distanza dal centro a qualsiasi punto sulla circonferenza è nota come raggio.
La formula dell’area
La formula per calcolare l’area del cerchio è data da:
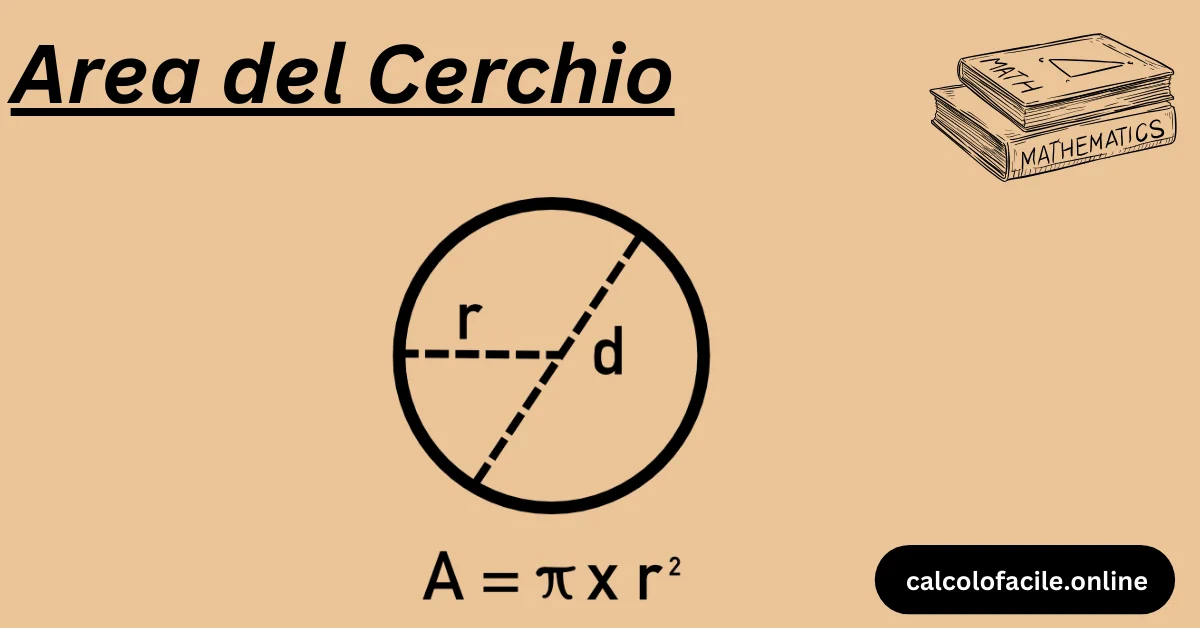
A=π×r2A = \pi \times r^2A=π×r2
dove AAA rappresenta l’area e rrr il raggio del cerchio. Il valore di π\piπ è una costante matematica approssimativamente uguale a 3,14159.
3. Calcolo dell’Area
Metodo base
Per calcolare l’area del cerchio, è sufficiente misurare il raggio e applicare la formula sopra. Ad esempio, se il raggio di un cerchio è 5 cm, l’area sarà:
A=π×52=25π≈78,54 cm2A = \pi \times 5^2 = 25\pi \approx 78,54 \, \text{cm}^2A=π×52=25π≈78,54cm2
Esempio pratico
Immagina di avere un cerchio con un raggio di 10 cm. Utilizzando la formula, calcoliamo l’area:
A=π×102=100π≈314,16 cm2A = \pi \times 10^2 = 100\pi \approx 314,16 \, \text{cm}^2A=π×102=100π≈314,16cm2
Esercizi e soluzioni
Gli esercizi pratici possono includere il calcolo dell’area di cerchi con raggi dati, la risoluzione di problemi reali come la determinazione dell’area di una pista ciclabile, e altro ancora.
4. Proprietà del Cerchio
Raggio e diametro
Il raggio è la distanza dal centro alla circonferenza, mentre il diametro è la distanza attraverso il cerchio passando per il centro. La relazione tra il raggio e il diametro è:
d=2rd = 2rd=2r
Circumferenza
La circumferenza del cerchio è la lunghezza della sua circonferenza ed è calcolata con:
C=2πrC = 2\pi rC=2πr
Settori e archi
Un settore del cerchio è una porzione di cerchio delimitata da due raggi e l’arco che li unisce. La misura dell’angolo al centro determina l’ampiezza dell’arco e l’area del settore.
5. Applicazioni Pratiche
In geometria
In geometria, l’area del cerchio viene utilizzata per risolvere problemi riguardanti la misurazione e la divisione delle superfici circolari.
In ingegneria
In ingegneria, la conoscenza dell’area del cerchio è fondamentale per la progettazione di elementi circolari, come tubi e ruote.
In architettura
Gli architetti utilizzano il concetto di area del cerchio per progettare strutture circolari e spazi architettonici.
6. Case Study e Applicazioni Reali
Studi di caso
Gli studi di caso possono includere la progettazione di edifici con strutture circolari o l’analisi di strutture esistenti come rotatorie e serbatoi.
Applicazioni industriali
Nelle applicazioni industriali, la misura precisa dell’area del cerchio è cruciale per la produzione di componenti circolari e per l’ottimizzazione dei processi di produzione.
7. Tendenze Future
Innovazioni nella geometria del cerchio
Le innovazioni nella geometria del cerchio possono includere nuove scoperte matematiche e tecniche di calcolo avanzate.
Nuove tecnologie e strumenti
Le nuove tecnologie, come i software di modellazione 3D, facilitano il calcolo e l’analisi dell’area del cerchio con maggiore precisione e efficienza.
8. Conclusione
In sintesi, comprendere l’area del cerchio è essenziale non solo per la matematica, ma anche per molte applicazioni pratiche. Dall’ingegneria all’architettura, il concetto di cerchio e la sua area sono fondamentali per risolvere problemi reali e innovare in vari campi.