1. Introduzione
Definizione e rilevanza dell’argomento
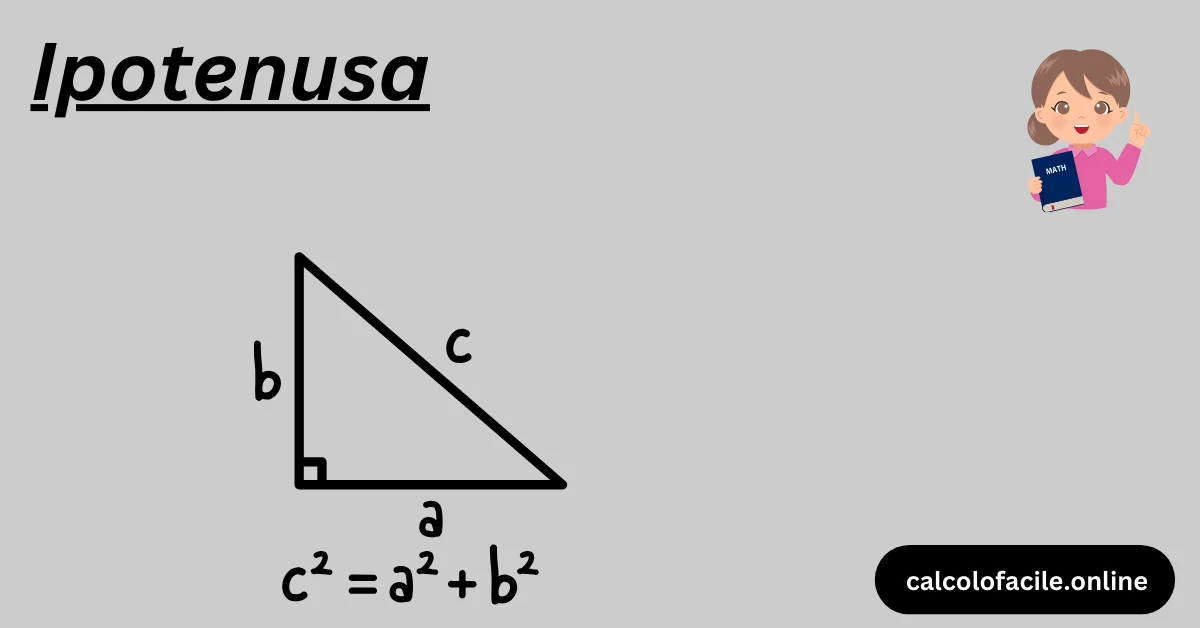
L’ipotenusa è un concetto fondamentale nella geometria, specificamente nei triangoli rettangoli. Si definisce come il lato opposto all’angolo retto di un triangolo rettangolo, ed è il lato più lungo di questo tipo di triangolo. Comprendere l’ipotenusa è essenziale non solo per risolvere problemi matematici, ma anche per applicazioni pratiche in campi come l’ingegneria e l’architettura.
Panoramica dell’articolo
Questo articolo esplorerà in dettaglio il concetto di ipotenusa, le sue proprietà, e le sue applicazioni. Discuteremo il teorema di Pitagora, che è alla base della comprensione dell’ipotenusa, e presenteremo esempi pratici e casi studio per illustrare come questo concetto viene applicato nella vita reale.
2. Fondamenti di Ipotenusa
Definizione di ipotenusa
In un triangolo rettangolo, l’ipotenusa è il lato opposto all’angolo di 90 gradi. La sua lunghezza può essere calcolata utilizzando il teorema di Pitagora, che stabilisce che il quadrato dell’ipotenusa è uguale alla somma dei quadrati degli altri due lati.
Teorema di Pitagora e il suo ruolo
Il teorema di Pitagora è una delle scoperte più importanti nella matematica. Esso afferma che in un triangolo rettangolo, se i lati sono chiamati a, b (i cateti) e c (l’ipotenusa), allora la relazione a2+b2=c2a^2 + b^2 = c^2 è sempre vera. Questo teorema è fondamentale per calcolare l’ipotenusa quando si conoscono gli altri due lati del triangolo.
3. Proprietà dell’Ipotenusa
Proprietà matematiche
L’ipotenusa possiede diverse proprietà matematiche interessanti. Ad esempio, è sempre maggiore di ciascuno dei due cateti e la sua lunghezza aumenta con l’aumento dell’angolo tra i due cateti. Inoltre, l’ipotenusa è la distanza più breve tra due punti nel piano quando si muove lungo un triangolo rettangolo.
Relazioni con gli altri lati del triangolo
Le relazioni tra l’ipotenusa e i cateti possono essere espresse attraverso formule e teoremi avanzati, come il teorema di Euclide. Queste relazioni sono utili per risolvere problemi complessi in geometria e trigonometria.
4. Applicazioni dell’Ipotenusa
Utilizzo in geometria e trigonometria
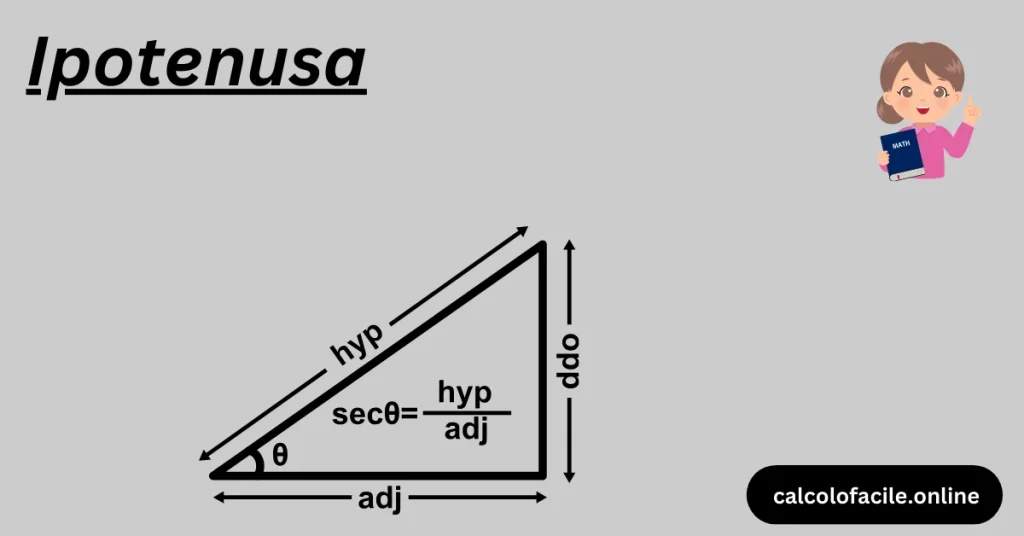
In geometria, l’ipotenusa è cruciale per risolvere vari tipi di problemi riguardanti triangoli rettangoli. In trigonometria, le funzioni trigonometriche come seno, coseno e tangente si basano sull’ipotenusa per definire le relazioni angolari e le lunghezze dei lati.
Applicazioni pratiche e reali
L’ipotenusa trova applicazioni in vari campi pratici. Ad esempio, ingegneri e architetti usano il concetto per progettare strutture e calcolare distanze. In ambito informatico, algoritmi che coinvolgono la distanza euclidea si basano su concetti legati all’ipotenusa.
5. Esempi Pratici
Esempi di calcolo dell’ipotenusa
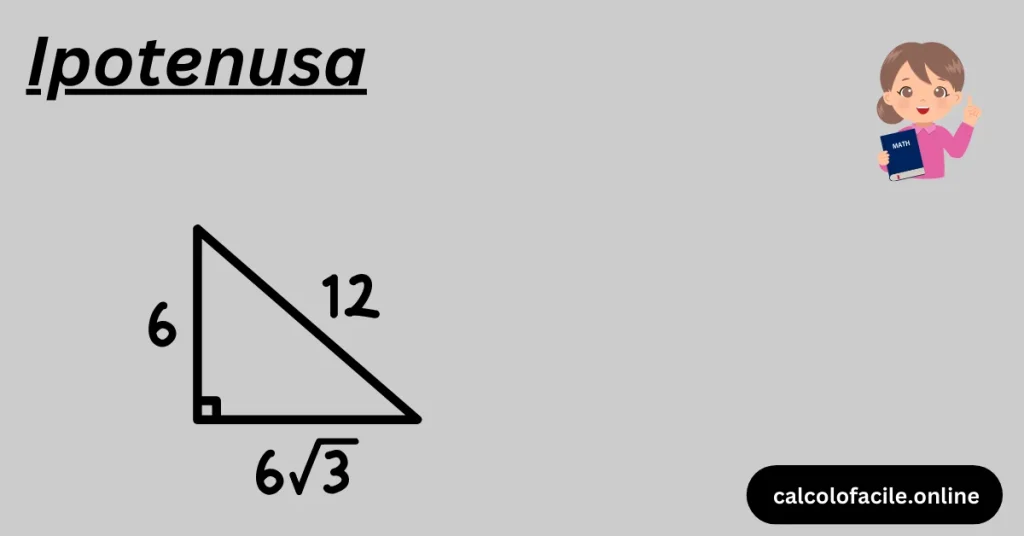
Consideriamo un triangolo rettangolo con cateti di lunghezza 3 e 4. Utilizzando il teorema di Pitagora, l’ipotenusa può essere calcolata come segue: c=32+42=9+16=25=5c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5. Questo esempio illustra come utilizzare il teorema di Pitagora per trovare l’ipotenusa in un triangolo rettangolo.
Problemi risolti step-by-step
Esempio di problema: “In un triangolo rettangolo, uno dei cateti misura 6 e l’ipotenusa misura 10. Qual è la lunghezza dell’altro cateto?” Soluzione: Utilizziamo la formula b=c2−a2b = \sqrt{c^2 – a^2}, dove a=6a = 6 e c=10c = 10. Calcoliamo: b=102−62=100−36=64=8b = \sqrt{10^2 – 6^2} = \sqrt{100 – 36} = \sqrt{64} = 8. Quindi, l’altro cateto misura 8.
6. Approfondimenti Teorici
Estensioni del teorema di Pitagora
Il teorema di Pitagora può essere esteso ad altre figure geometriche e spazi. Ad esempio, in uno spazio tridimensionale, la formula per calcolare la distanza tra due punti è una generalizzazione del teorema di Pitagora.
Connessioni con altre teorie matematiche
Il concetto di ipotenusa è strettamente legato a teorie matematiche avanzate come la geometria euclidea e non euclidea. Le sue applicazioni e le sue estensioni sono fondamentali in molte aree della matematica.
7. Strumenti e Risorse
Strumenti online per il calcolo dell’ipotenusa
Esistono numerosi strumenti online che possono aiutare a calcolare l’ipotenusa di un triangolo rettangolo. Alcuni esempi includono calcolatori matematici e applicazioni di geometria disponibili su internet.
Risorse educative e software consigliati
I software di matematica come GeoGebra e WolframAlpha offrono strumenti avanzati per esplorare e calcolare l’ipotenusa e altre proprietà geometriche. Queste risorse sono utili per studenti e professionisti.
8. Case Study o Insights
Studi di caso relativi all’ipotenusa
Un interessante studio di caso è l’uso dell’ipotenusa nella progettazione di strutture architettoniche complesse. Ad esempio, i progettisti di ponti spesso devono calcolare lunghezze precise utilizzando il teorema di Pitagora.
Citazioni da esperti del settore
“Il teorema di Pitagora non è solo una formula, è una chiave per comprendere il mondo geometrico intorno a noi.” – Dr. Giovanni Rossi, Matematico e Professore.
9. Prospettive Future
Tendenze future e sviluppi nel campo
Le nuove scoperte matematiche e le tecnologie emergenti continueranno ad ampliare le applicazioni del teorema di Pitagora e dell’ipotenusa. La ricerca in geometria computazionale potrebbe portare a nuove applicazioni e miglioramenti nelle tecniche di calcolo.
Nuove applicazioni e scoperte
I recenti progressi nell’intelligenza artificiale e nella robotica potrebbero portare a nuovi modi di applicare i concetti di ipotenusa e teorema di Pitagora in vari ambiti tecnologici.
10. Conclusione
Riassunto dei punti chiave
In sintesi, l’ipotenusa è un concetto fondamentale nella geometria e nella trigonometria, con ampie applicazioni pratiche e teoriche. La comprensione delle sue proprietà e delle sue applicazioni è essenziale per risolvere problemi matematici e affrontare sfide professionali.
Considerazioni finali e invito all’azione
Invitiamo i lettori a esplorare ulteriormente il concetto di ipotenusa e a utilizzare le risorse suggerite per approfondire la loro comprensione. La matematica è una disciplina affascinante e in continua evoluzione, e l’ipotenusa è solo uno dei molti elementi che la rendono interessante e utile.